Veranstaltungen und Projekte

„Grundlagen der Kryptographie: Wie man einen geheimen Schlüssel abhörsicher vereinbart“ – das war der Titel des Workshops, an dem die Klassen 5a und 5b am 24. Mai teilnehmen durften. Frau Kurth und Frau Bayer-Eynck hatten dafür das MINTmobil eingeladen. Mit Schatzkisten und einem digitalen Schlüsseltausch auf den Tablets konnten die Schüler*innen das Thema „Krypthographie“ spielerisch vertiefen. Sie haben dabei einen Einblick bekommen, wie die Sicherheit beim Austausch von Daten erhöht werden kann. Die Kenntnis der Grundlagen von Verschlüsselungsverfahren soll den Schüler*innen eine genauere Beurteilung des Grades der Sicherheit ermöglichen.

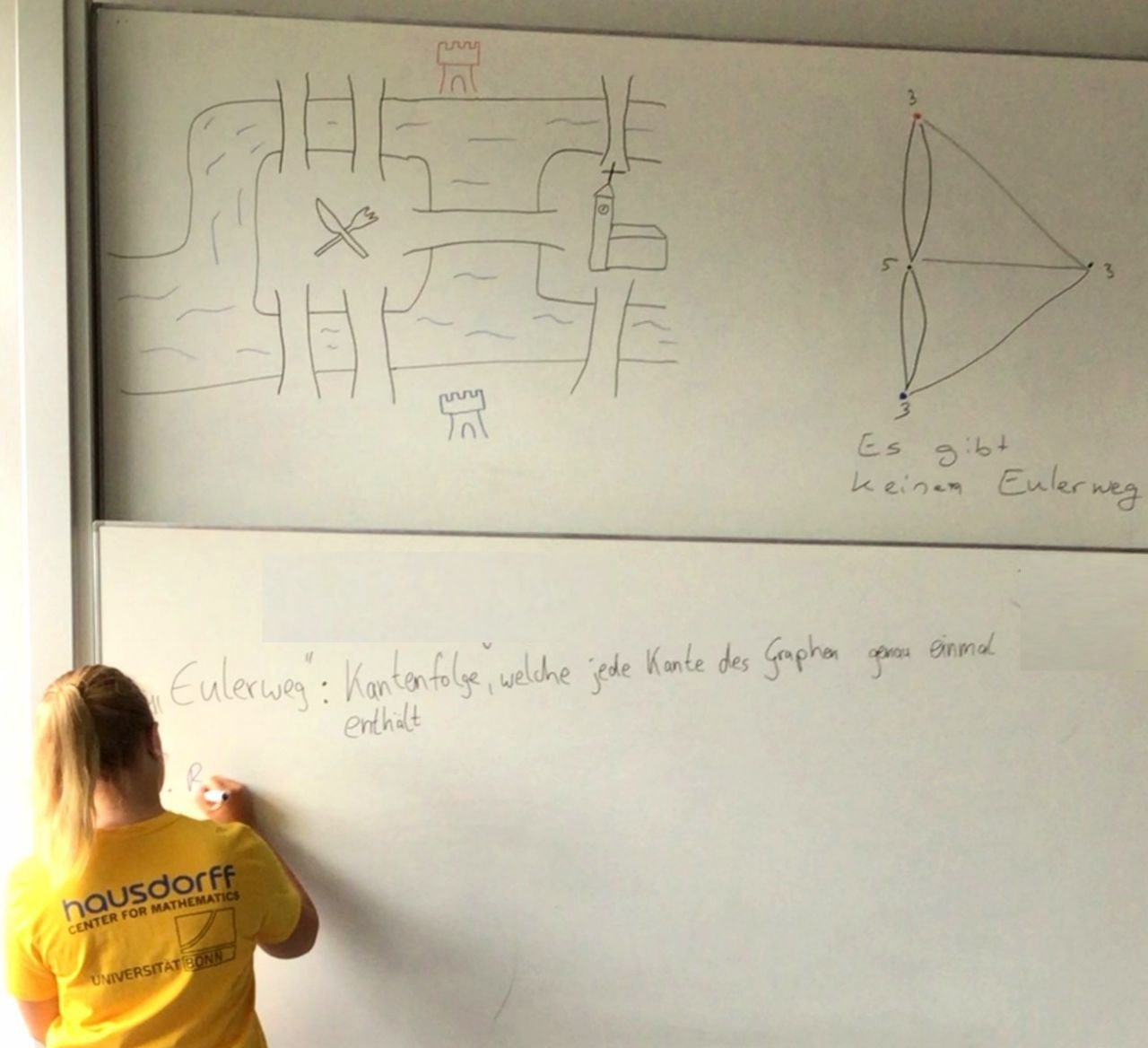
Das Haus vom Nikolaus haben sich drei sechste Klassen im Juni 2022 genauer angesehen: Was ist eigentlich das Besondere daran – und (was) hat es mit Mathematik zu tun? Im Rahmen der von Frau Bayer-Eynck organisierten Zusammenarbeit mit dem Hausdorff Center for Mathematics wurden diese Aspekte eingehend untersucht. Hierdurch wurden die Schüler*innen spielerisch an das Gebiet der Graphentheorie herangeführt. Auch fernab des bekannten Nikolaushäuschens gab es spannende Themen: Lassen sich etwa alle sieben Königsberger Brücken bei einem Rundgang durch die Stadt überqueren? Diese Frage, die Leonard Euler bereits 1736 umtrieb, können die Sechstklässler nun jedenfalls beantworten. Herzlicher Dank an das Schulteam des HCM für die gelungenen Workshops!